Teoría elemental de la probabilidad

La teoría de la probabilidad es la parte de las matemáticas que estudia los fenómenos aleatorios cuyo comportamiento es intrínsecamente no determinista. O bien, en dónde está involucrado el azar.

DIAGRAMA DE ÁRBOL
Un diagrama de árbol es el dibujo que se usa para enumerar todos los resultados posibles de una serie de experimentos en donde cada experimento puede en un numero finito de maneras.

Un diagrama de árbol es una representación gráfica de un experimento que consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.
Ejemplo
Queremos calcular los sucesos elementales que resultan al lanzar dos veces una moneda.

Como podemos observar se llevan a cabo 2 experimentos (lanzamientos de moneda) en los cuales se pueden obtener p^n resultados diferentes, dónde p es la cantidad de resultados posibles y n la cantidad de experimentos realizados.

PROBABILIDAD DE EVENTOS
Un evento dentro de un entorno de probabilidades es la cantidad de veces que ocurre un determinado suceso dentro de un cierto número de observaciones (experimentos). O bien es un subconjunto de probabilidades dentro de un espacio muestral.

Para calcular un evento es necesario saber 2 cosas:
n: Cantidad de experimentos
x: Cantidad de veces que ocurrió el evento

p(x) = x/n

Video: Probabilidad de un evento simple

Ejemplo
El ejemplo más básico es el lanzamiento de una moneda; supongamos que lanzamos la moneda 10 veces, de las cuales 4 cayeron en cara y 6 en cruz,
la probabilidad de que salga cara es de 4/10 = 0.4 = 40%.

PROBABILIDAD CONDICIONALEs la probabilidad de que ocurra un evento dado que ha ocurrido otro antes que este y el segundo depende del resultado del primero.

P(B|A): Probabilidad de que ocurra B dado A
B: Evento dependiente
A: Evento independiente




Ejemplo

En una tómbola hay 12 esferas rojas y seis negras. Si se sacan dos en forma consecutiva, sin reponer la primera, ¿cuál es la probabilidad de que la primera sea roja y la segunda sea negra?
La probabilidad de que la primera sea roja es 12/18 y de que la segunda sea negra, dado que la primera fue roja, es 6/17, por lo tanto:

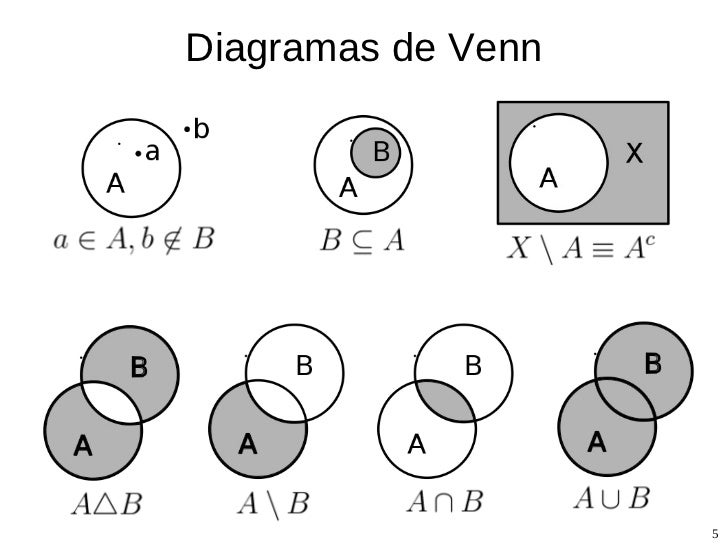
DIAGRAMAS DE VENN

Los diagramas de Venn son comúnmente utilizados para la representación gráfica de uno o más conjuntos de datos dentro de un espacio muestral, dónde se encierra el contenido de cada conjunto y todos los diagramas son encerrados en el denominado Universo.

En un diagrama se puede representar varias operaciones de conjuntos tales como:
Unión: U
Intersección: ∩
Pertenencia: ⊂
Exclusión: ⊄
Diferencia: \
Complemento: A‟
Conjunto nulo: ⃠

 

Ejemplo
De una encuesta hecha a 135 personas para establecer preferencias de lectura de las revistas A, B y C; se obtienen los siguientes resultados:

Todos leen alguna de las 3 revistas; todos, menos 40, leen A; 15 leen A y B pero no C, 6 leen B y C pero no A; 10 leen sólo C. El número de los que leen A y C es el doble del número de los que leen las 3 revistas. El número de los que leen sólo B es el mismo que el total de los que leen A y C. Según todo esto, hallar el número de los que leen solamente A.